精密位置測定用位相 補正付きローパス・フィルタ
日本キャステム株式会社 技術営業顧問
株式会社制振技術研究所 代表取締役
奥屋嗣之 著
もくじ
はじめに
連続移動するステージ等の位置を精密に検出する必要がある場合に,測定データのノイズ成分を除去する必要があります。 そのノイズ成分の除去をするために,ローパス・フィルタの使用を考えてみます。 除去すべきノイズ成分の周波数が極めて高く,ローパス・フィルタの時定数が十分に小さい場合は問題ありませんが, そうでない場合はステージ速度に時定数を乗じた位置ずれが発生し,この位置ずれを補正する必要があります。 また,ステージ速度が変動する場合には,その変動による位置ずれの補正も必要となります。 比較的低い周波数領域のノイズ成分が問題となるケースとして,ステージの精密位置測定用に用いられるレーザ干渉計の非線形誤差成分があります。 この非線形誤差成分はレーザ干渉計の光学系に由来するもので,レーザ波長の1/4又は1/2の位置依存変動成分であり, 通称ラムダエラー(λエラー)と言われています。 ラムダエラーは移動速度に比例した周波数のノイズ成分として検出され,レーザ波長とステージ走行速度にもよりますが, 数kHz ~ 数百kHzの周波数領域となります。 ここで紹介するのは,このようなニーズに対して具体的な解決手段を提供することが出来るデジタル・フィルタの技術内容です。
位相補正付きローパスフィルターの構成と特性
変位入力に対して速度補正,あるいは加速度補正, 加加速度補正等を行う位相補正付きローパス・フィルタの基本構成を「図2.1」に示します。変位入力に対して速度補正,あるいは加速度補正, 加加速度補正等を行う位相補正付きローパス・フィルタの基本構成を「図2.1」に示します。
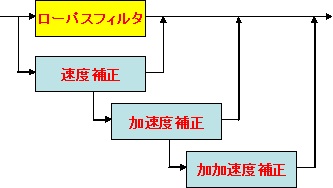
(図2.1)位相補正付きローパス・フィルタの基本構成(図2.1)
位相補正付きローパス・フィルタの基本構成ローパス・フィルタに対して速度補正を行うには,ハイパス・フィルタを用いることとなりますが, 単純に時定数を同じにしてパラレル配置するとスルーパス・フィルタとなってしまいます。 そこでハイパス・フィルタにローパス・フィルタを乗じたものをパラレル配置することで速度補正が可能となります。 加速度補正,加加速度補正等も同様な考え方で構成することができます。 以下に位相補正付きローパス・フィルタの伝達関数とフィルタ特性の例を,通常の1次ローパス・フィルタと比較して示します。 なお,図中の赤線が通常の1次ローパス・フィルタの特性です。
速度補正付き1次ローパス・フィルタ
速度補正付き1次ローパス・フィルタの伝達関数を「式2.1」に,周波数特性の例(fc=1kHz)を「図2.2」および「図2.3」に示します。
(式2.1)
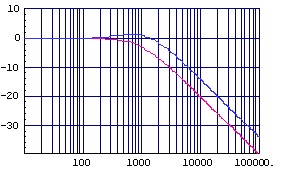
(図2.2)速度補正付きゲイン特性(縦:dB,横:Hz)
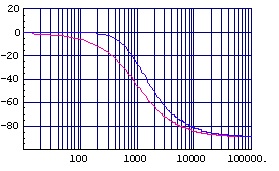
(図2.3)速度補正付き位相特性(縦:deg,横:Hz)
加速度補正付き1次ローパス・フィルタ
加速度補正付き1次ローパス・フィルタの伝達関数を「式2.2」に,周波数特性の例(fc=1kHz)を「図2.4」および「図2.5」に示します。
(式2.2)
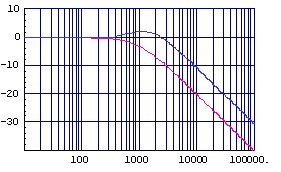
(図2.4)加速度補正付きゲイン特性(縦:dB,横:Hz)
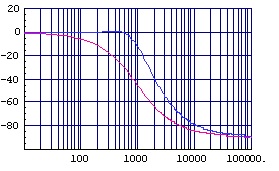
(図2.5)加速度補正付き位相特性(縦:deg,横:Hz)
加加速度補正付き1次ローパス・フィルタ
加加速度補正付き1次ローパス・フィルタの伝達関数を「式2.3」に,周波数特性の例(fc=1kHz)を「図2.6」および「図2.7」に示します。
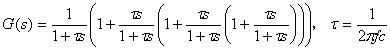
(式2.3)
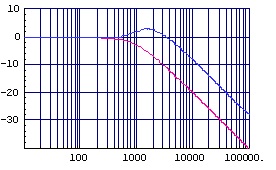
(図2.5)加加速度補正付きゲイン特性(縦:dB,横:Hz)
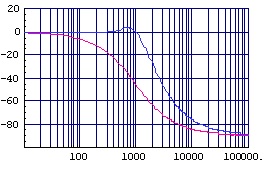
(図2.6)加加速度補正付き位相特性(縦:deg,横:Hz)
ステージ走行時の位置ずれ
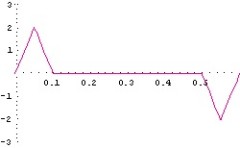
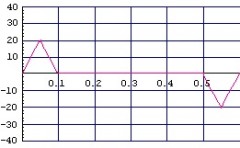
- (図3.1)位置ずれシミュレーション計算用 ステージ加速度パターン(縦:G, 横:sec)
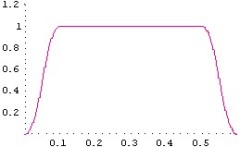
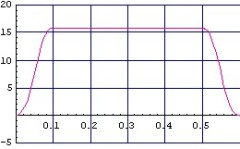
- (図3.2)位置ずれシミュレーション計算用 ステージ速度パターン(縦:m/s, 横:sec)
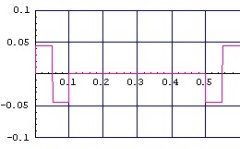
- (図3.3)通常のローパス・フィルタ 位置ずれ(縦:μm, 横:sec)
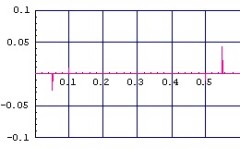
- (図3.4)速度補正ローパス・フィルタ 位置ずれ(縦:nm, 横:sec)
- (図3.5)加速度補正ローパス・フィルタ 位置ずれ(縦:nm, 横:sec)
- (図3.6)加加速度補正ローパス・フィルタ 位置ずれ(縦:nm, 横:sec)
(表3.1)各種1次ロ-パス・フィルタの位置ずれ比較
| 位相補正 | カットオフ周波数(fc) | 位置ずれ |
|---|---|---|
| 補正無し | 10.0kHz | 16μm |
| 速度補正付き | 5.0kHz | 20nm |
| 加速度補正付き | 3.3kHz | 0.045nm |
| 加加速度補正付き | 2.5kHz | (0.043nm) |
高次補正をすることで飛躍的に位置ずれを小さくすることができます。 なお,このシミュレーション計算においてはステージ走行パターンの加加速度が不連続となるため, 加加速度補正に対する計算結果には信憑性がありません。 実際のステージ走行時には加加速度が不連続となることがありません。 よって,ステージ駆動系のモデルを構築し, ステージ走行パターンに対するステージの応答解析をすることで加加速度補正においても正当な評価を得ることができます。(ここでは割愛します。)
デジタル・フィルタの係数精度と量子化誤差対策
位相補正付きローパス・フィルタを実現するためには伝達関数を離散化し,演算遅延時間を最低限に抑えられるようにします。 よって,高速大容量演算素子FPGAを用いたIIR方式のデジタル・フィルタが必要です。
IIRフィルタはFIRフィルタに比べ演算遅延時間が短いのが利点ですが,フィードバック系の演算であるため,サンプリングタイムと時定数の比が大きい場合,その比とフィルタ次数に比例した係数精度(有効桁数)が必要となります。
フィルタ係数の精度が不十分な場合,量子化誤差(離散化に伴う桁落ち誤差)により,演算結果が発散してしいます。 このため,ステップ応答に対する収束性をシミュレーションで計算し,フィルタ係数の末尾を調整することによってデジタル化した場合の量子化誤差対策を行います。